【科学基础】声音的物理本质与能量的基本数学表达式

EQ（Equalization，均衡器）本质上是一个频率选择性的增益函数：

频谱图（如 Ableton 的 Spectrum、FabFilter 的 Analyzer）实时显示 X(f)；EQ 滤波器实际影响的是 H(f)；混音时，我们观察频谱并视觉定位问题频段，然后手动绘制 H(f) 来进行补偿或增强。

EQ 不是“修音”，是“重塑频率能量分布”，本质是用数学曲线，对声音进行“能量雕刻”。

它作用于信号的频谱，在特定频率区域 放大（Boost） 或 削减（Cut） 能量。

【音频技术】什么是EQ均衡器( Equalizer )？有哪些类型？【图文详解】

在数学上：

一个 EQ 可以看作是一个 线性时不变系统（LTI），其效果可用卷积描述：

y(t) = x(t) * h(t)

其中：
x(t) 是输入信号
h(t) 是 EQ 的脉冲响应
* 表示卷积运算
y(t) 是处理后的输出信号

频谱角度看 EQ

信号的频谱是通过 傅立叶变换（Fourier Transform） 获得的：

X(f) = ∫ x(t) * e^(-j2πft) dt

应用 EQ 实际上就是将一个频谱 X(f) 乘以一个频率响应 H(f)：

Y(f) = X(f) × H(f)

换句话说：EQ 就是在频域上进行的乘法滤波，每个 EQ 滤波器类型对应一个特定形状的频率响应 H(f)。

音频压缩器的工作原理算法

可以从动态范围压缩（dynamic range compression）的数学角度来描述，它的核心是在音频信号达到某个阈值（threshold）后，对超出的部分进行缩减，按照一定的压缩比（ratio）计算。

「科学基础」音频压缩器的四种变体运行原理以及应用场景

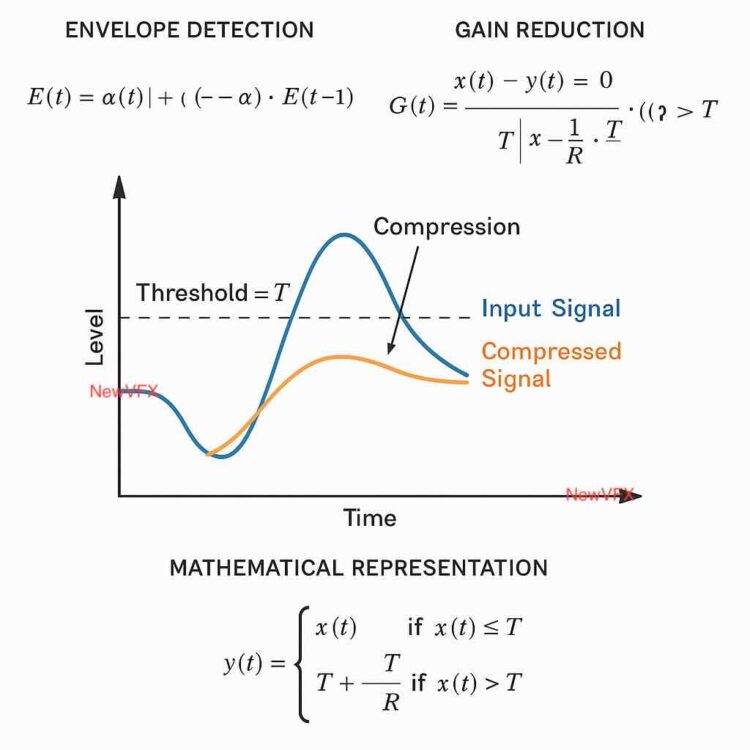
音频压缩器数学算法图解（由NewVFX结合AI制作）

1. 基本压缩表达式

设：
x(t)：输入信号的幅度（通常是 dBFS）
T：压缩器的阈值（threshold，单位为 dB）
R：压缩比（ratio，例如 4:1 则 R = 4）
y(t)：输出信号的幅度（单位为 dB）

压缩器的工作逻辑可以表达为：

\(
y(t) =
\begin{cases}
x(t), & \text{if } x(t) \leq T \
T + \frac{x(t) – T}{R}, & \text{if } x(t) > T
\end{cases}
\)

解释：
当信号小于等于阈值时，保持原样；
当信号超过阈值时，超出部分被按比例压缩。

2、增益变化（Gain Reduction）

计算增益衰减值：

\(
G(t) = x(t) – y(t) =
\begin{cases}
0, & x(t) \leq T \
\left(1 – \frac{1}{R} \right)(x(t) – T), & x(t) > T
\end{cases}
\)

3. 包络检测（Envelope Detection）

为了避免点击声和非线性突变，压缩器会对信号包络进行平滑处理（Attack/Release 时间），用指数平滑滤波器：

\(
E(t) = \alpha \cdot |x(t)| + (1 – \alpha) \cdot E(t – 1)
\)

其中：
\(\alpha = 1 – e^{-\frac{1}{\tau f_s}}；\tau 是时间常数（Attack 或 Release）；f_s 是采样率\)

压缩算法归纳：
压缩器是一种非线性动态处理器，其核心算法涉及：
条件判断（大于阈值即压缩）

线性缩放（压缩比率）
时间平滑（包络追踪）

它既有数学公式上的逻辑推导，也有声音行为上的艺术性。

Oversampling（过采样）在数字信号处理中常用的数学表达式

Oversampling（过采样）的数学原理及其在音频处理中的应用，包括插零、低通滤波和降采样的完整表达式。掌握高保真音频插件如何通过过采样减少失真与折叠噪声，提升声音质量。Oversampling（过采样）在数字信号处理中有明确的数学定义和实现过程。

音频处理插件的 Oversample 模式的优势以及应用场景

以下是核心原理和常用的数学表达式：

1. 过采样因子定义
数学表达式

设：

• \(x[n]\)：原始离散时间信号（采样率为 \(f_s\)）
• \(L\)：过采样因子（如 2x, 4x）

则 Oversampled 信号 \(x_L[n]\) 的生成可表达为：

\(
x_L[n] =
\begin{cases}
x\left[\frac{n}{L}\right], & n \equiv 0 \pmod{L} \\
0, & \text{otherwise}
\end{cases}
\)

意思是：在原始采样点之间插入 \(L – 1\) 个零（零插值）。

2. 插值滤波（Interpolation Filtering）

为了平滑插值后的信号，需要一个低通滤波器 \(h[n]\)：

\(x_{int}[n] = x_L[n] * h[n]\)

其中 \(*\) 表示卷积，滤波器截止频率为：

\(f_c = \frac{f_s}{2}\)

3. 降采样（后期处理）

在 Oversampling 处理完毕后，进行降采样操作：

\(y[n] = x_{int}[nL]\)

总结流程

1. 插零：

   \(x_L[n] = x[n/L], \text{（插零）}\)

2. 滤波：

   \(x_{int}[n] = x_L[n] * h[n]\)

3. 降采样：

   \(y[n] = x_{int}[nL]\)

混响的物理与数学原理详解

🎵 混响是声音在空间内多次反射并衰减的现象，是营造音频空间感和自然感的重要元素。

物理本质

• 声音在封闭或半封闭空间传播，遇到墙壁、地面、天花板等表面产生反射。
• 初级反射（Early Reflections）：最先到达耳朵的几次较强反射，帮助感知空间大小。
• 混响尾声（Reverberation Tail）：大量次级反射叠加形成的持续衰减声音，赋予空间“丰满感”。

数学模型描述

🔍 混响可看作线性时不变系统（LTI），空间对声音的作用由脉冲响应（Impulse Response，IR）描述。

• 输入声音信号为 \( x(t) \)
• 空间脉冲响应为 \( h(t) \)
• 输出声音为两者的卷积：\( y(t) = x(t) * h(t) = \int_{-\infty}^{\infty} x(\tau) \cdot h(t-\tau) \, d\tau \)

脉冲响应特点

• 直接声对应脉冲响应中第一个冲击。
• 初级反射表现为几个较大幅度的离散峰值。
• 混响尾声由大量微弱反射组成，幅度随时间指数衰减。
• 数学表达：\( h(t) = \sum_{i=1}^N a_i \cdot \delta(t – \tau_i), \quad a_i \to 0 \text{ 随 } \tau_i \to \infty \)

混响衰减模型

⏳ 混响尾声衰减通常用指数函数描述：

\( a(t) = a_0 e^{-t / \tau} \)

• \( a_0 \) 是初始幅度
• \( \tau \) 是衰减时间常数，反映空间吸收特性
• 混响时间 RT60 是声音衰减 60 dB 所需时间，衡量空间混响强弱

数字音频工作站（DAW）中的混响实现

• 卷积混响（Convolution Reverb）：利用真实空间的脉冲响应进行卷积，实现高度真实的空间效果，计算量大。
• 算法混响（Algorithmic Reverb）：使用反馈延迟网络、多级滤波器等数学模型模拟混响，灵活且计算效率高。

算法混响示例

🔄 简单反馈延迟模型：

\( y[n] = x[n] + g \cdot y[n – D] \)

• \( D \)：延迟样本数，决定反射时间
• \( g \)：反馈增益，控制衰减速度
• 通过组合多个此类单元形成复杂混响尾声